CplexA tutorial (Matlab implementation)

Jose M. G. Vilar 1,2 and Leonor Saiz 3

1. Biophysics Unit (CSIC-UPV/EHU) and Department of Biochemistry and Molecular Biology, University of the Basque Country, P.O. Box 644, 48080 Bilbao, Spain

2. IKERBASQUE, Basque Foundation for Science, 48011 Bilbao, Spain

3. Department of Biomedical Engineering, University of California, 451 East Health Sciences Drive, Davis, CA 95616, USA

SUMMARY:

CplexA is a software package (available for Mathematica, Python, and Matlab) to study the effects of macromolecular assembly on cellular processes. A main challenge for conventional computational methods to study macromolecular assembly is tackling the exponential increase of the number of configurational states with the number of components. CplexA uses functional programming to efficiently compute probabilities and average properties over such exponentially large number of states from the energetics of the interactions. The package is particularly suited to study gene expression at complex promoters controlled by multiple, local and distal, DNA binding sites for transcription factors. CplexA is freely available at http://sourceforge.net/projects/cplexa/.

REFERENCES:

1. The main reference for CplexA is Vilar, J.M.G. and Saiz, L. (2010) CplexA: a Mathematica package to study macromolecular-assembly control of gene expression, Bioinformatics 26, 2060-2061.

2. The biophysical background of the methods used by CplexA are described in Saiz, L. and Vilar, J.M.G. (2006) Stochastic dynamics of macromolecular-assembly networks, Mol Syst Biol, 2, 2006.0024.

Contents

Running the tutorial

To run the python tutorial, the file AveConf.m must be in the Path, the default list of directories searched by Matlab to find an external file. CplexA uses the Symbolic Math Toolbox.

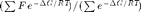The main function of CplexA is AvConf(F, $\Delta$ G, S, RT)= $(\sum F e^{-\Delta G/RT})/ (\sum e^{-\Delta G/RT})$, which efficiently computes the thermodynamic average of F for a system with free energy $\Delta$ G described by the set S of state variables. The function returns a symbolic expression and the terms F, $\Delta$ G, S, and RT can be symbolic or string expressions. Each state variable can take the values 0 or 1 to represent whether a property is present or not. Both F and $\Delta$ G are functions of S. RT is the thermal energy (gas constant, R, times the absolute temperature, T). The sums are performed over all possible combinations of values of the state variables.

Note that different units can be used for the thermal energy, for instance kT (AvConf(F, $\Delta$ G, S, kT)) or even numerical values explicitly (AvConf(F, $\Delta$ G, S, 0.6)). The three-argument function AvConf(F, $\Delta$ G, S) assumes RT as a default thermal energy.

An activator

A transcription factor with concentration n1 binds a DNA site described by the state variable s1. The variable indicates whether (s1=1) or not (s1=0) the transcription factor is bound. S is the set of state variables describing the system (in this case, it consists only of s1); DG is the free energy of the system; DG0 is the standard free energy of binding at 1M; and F is the transcription rate, which is Fmax when the transcription factor is bound (s1=1) or zero when it is not (s1=0).

The example below computes the average transcription rate AF.

S='s1';
DG='(DG0-RT*log(n1))*s1';
F='Fmax*s1';
AF=AveConf(F,DG,S);

disp(simplify(AF))

(Fmax*n1)/(n1 + exp(DG0/RT))

Same example as before, but now the free energy is expressed in terms of the dissociation constant Kd (recall the equivalency 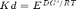$Kd=E^{DG^o/RT}$ :

DG='-RT*log(n1/Kd)*s1';
AF=AveConf(F,DG,S);

disp(AF)

(Fmax*n1)/(Kd + n1)

Two molecules binding to overlapping sites

Two molecules with concentrations n1 and n2 compete for binding to overlapping sites (binding of one excludes the binding of the other). The variables s1 and s2 indicate whether molecules 1 and 2 are bound, respectively. The expression below computes the probability that molecule 1 is bound, which is given by the average value of s1.

Note the term inf s1 s2 in the free energy. It implements the logical condition that two molecules cannot be bound simultaneously by assigning an infinite free energy to the corresponding state. To obtain the correct thermodynamic result, the symbol inf is considered to be finite until the end result, and then the limit to infinity is taken.

AF=AveConf('s1','-RT*log(n1/K1)*s1-RT*log(n2/K2)*s2+inf*RT*s1*s2','s1 s2');

disp(simplify(AF))

(K2*n1)/(K2*n1 + K1*(K2 + n2))

Cooperative binding

Similar to the previous example, but now the binding of one does not exclude the other. The term e12 is the interaction energy between the molecules bound. The following expression computes the probability of having the two sites occupied simultaneously:

AF=AveConf('s1*s2','-RT*log(n1/K1)*s1-RT*log(n2/K2)*s2+e12*s1*s2','s1 s2');

disp(simplify(AF))

(n1*n2)/(exp(e12/RT)*(K1*n2 + K2*n1 + K1*K2 + (n1*n2)/exp(e12/RT)))

lac Operon

The lac repressor is a protein with two DNA binding domains. It can bind to one site or, by looping the intervening DNA, to two distal sites simultaneously.

In addition to the domain-binding state variables to each site, s1 and s2, there is a looping state variable sL that indicates wether the DNA is looped (sL=1) or not (sL=0). Note that the each binding domain at sites 1 and 2 can be from two different lac repressors or from a single one when there is looping. The term inf (1 - s1 s2) sL means that looping can only happen with two domains bound, otherwise the free energy is infinite. The following expression computes the repression level:

AF=AveConf('(1-s1)',['-RT*log(n/K1)*s1-RT*log(n/K2)*s2'...
          ,'+(gL+RT*log(n)*s1*s2)*sL+inf*RT*(1-s1*s2)*sL'],'s1 s2 sL');

disp(1+simplify(1/AF-1))
disp(1+simplify(1/subs(AF,'gL','-RT*log(cL)')-1))

(n*(K2 + n + 1/exp(gL/RT)))/(K1*(K2 + n)) + 1
 
(n*(K2 + cL + n))/(K1*(K2 + n)) + 1

Note that gL is the contribution to the free energy due to the conformational change of DNA (free energy of looping).

The repression level can also be expressed in terms of the local concentration cL, defined as 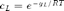$c_L=e^{-g_L/RT}$:

Phage $\lambda$

The CI protein of phage $\lambda$ can bind as a dimer to three sites on the right operator (described here by the state variables sOR1, sOR2, and sOR3 ) and to another three sites on the left operator (described by sOL1, sOL2, and sOL3). The state variable sL describes the looping state.

The free energy of the system DG takes into account interactions between CI dimers bound at neighboring sites and, when there is looping (sL=1), at different operators as well.

S='sOL1 sOL2 sOL3 sOR1 sOR2 sOR3 sL';
DG=['-2.5*sOL1*sOL2 - 2.5*sOL2*sOL3 + 2.5*sOL1*sOL2*sOL3'...
   ,'-3*sOR1*sOR2 - 3*sOR2*sOR3 + 3*sOR1*sOR2*sOR3'...
   ,'+ sL*(21 - 21.2*sOL1*sOL2*sOR1*sOR2 - 3*sOL3*sOR3)'...
   ,'+ sOL1*(-13.8 - RT*log(n)) + sOR1*(-12.7 - RT*log(n))'...
   ,'+ sOL3*(-12.4 - RT*log(n)) + sOL2*(-12.1 - RT*log(n))'...
   ,'+ sOR2*(-10.7 - RT*log(n)) + sOR3*(-10.2 - RT*log(n))'];

Transcription at the PRM promoter is given by F_rm, which leads to the average AF_rm. There is also another promoter, PR, with transcription given by F_r, which leads to the average AF_r.

F_rm='(45 + (415*(1 - sL) + 195*sL)*sOR2)*(1 - sOR3)';
AF_rm=AveConf(F_rm,DG,S);
AF_rm_n=simplify(subs(AF_rm,'RT',0.6));

disp(vpa(AF_rm_n,5))

(3.4779e51*n^5 + 3.974e42*n^4 + 1.2059e32*n^3 + 2.5187e22*n^2 + 6.0251e11*n + 45.0)/(2.1995e58*n^6 + 1.0843e49*n^5 + 1.2315e40*n^4 + 1.1504e30*n^3 + 4.3593e20*n^2 + 1.2901e10*n + 1.0)
 

F_r='1200*(1 - sOR1)';
AF_r=AveConf(F_r,DG,S);
AF_r_n=simplify(subs(AF_r,'RT',0.6));

disp(vpa(AF_r_n,5))

(8.1396e49*n^5 + 1.2926e41*n^4 + 4.499e32*n^3 + 4.8659e23*n^2 + 1.3611e13*n + 1200.0)/(2.1995e58*n^6 + 1.0843e49*n^5 + 1.2315e40*n^4 + 1.1504e30*n^3 + 4.3593e20*n^2 + 1.2901e10*n + 1.0)

Note that in both cases it is possible to obtain an exact analytical expression for the effective transcription rates, AF_rm and AF_r, as a function of the CI dimer concentration. The expression nvals below gives the CI dimer concentration from the normalized CI monomer concentration nnvals.

nnvals=(0:0.025:2.5);
nvals=9.38419e-14 + 7.0922e-10*nnvals - 1.15373e-11*sqrt(0.0000661586 + 1.*nnvals);

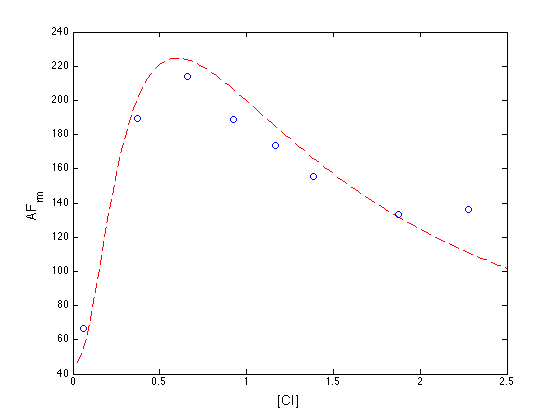
Plotted below is AF_rm (solid red line) as a function of the normalized CI monomer concentration. The circles correspond the experimentally measured activity of the PRM promoter (Dodd, I.B., Shearwin, K.E., Perkins, A.J., Burr, T., Hochschild, A.and Egan, J.B.(2004) Cooperativity in longrange gene regulation by the lambda CI repressor, Genes Dev, 18, 344-354).

PRMdata = [0.058, 66.367; 0.373, 189.358; 0.658, 214.233; 0.922, 188.897;...
           1.168, 173.696; 1.385, 155.271; 1.875, 133.160; 2.281, 136.384];
ff=matlabFunction(AF_rm_n);
plot(nnvals,ff(nvals),'r--',PRMdata(:,1), PRMdata(:,2),'ob');
xlabel('[CI]','fontsize',14); ylabel('AF_{rm}','fontsize',14);

Plotted below is AF_r (solid red line) as a function of the normalized CI monomer concentration. The circles correspond the experimentally measured activity of the PR promoter ( Dodd, I.B., Shearwin, K.E., Perkins, A.J., Burr, T., Hochschild, A.and Egan, J.B.(2004) Cooperativity in longrange gene regulation by the lambda CI repressor, Genes Dev, 18, 344 - 354).

PRdata = [0.063, 1057.627; 0.373, 585.763; 0.658, 204.746; 0.921, 70.508;...
          1.171, 27.119; 1.384, 18.983; 1.875, 12.203; 2.278, 9.492];
ff=matlabFunction(AF_r_n);
plot(nnvals,ff(nvals),'r--',PRdata(:,1), PRdata(:,2),'ob');
xlabel('[CI]','fontsize',14); ylabel('AF_{r}','fontsize',14);


Published with MATLAB® 7.13